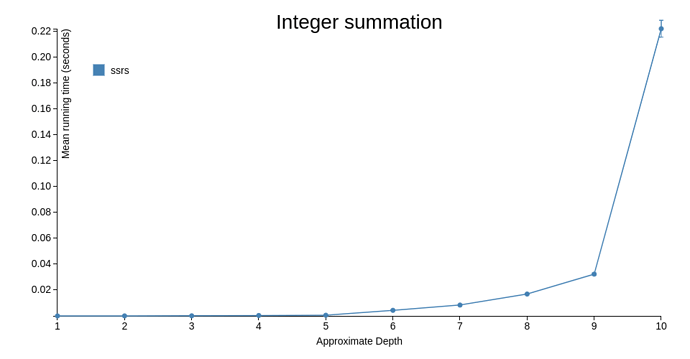
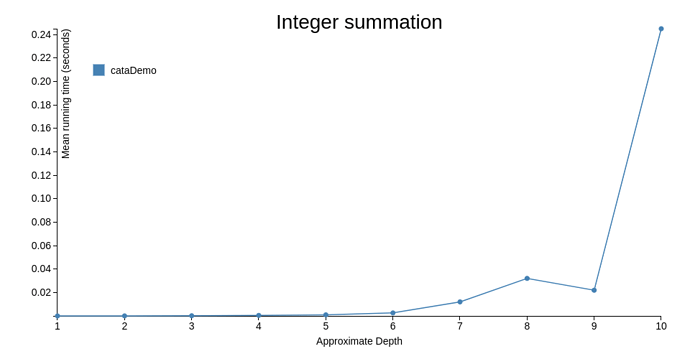
A while back, I implemented a library for functional dissections in PureScript with dissect, which then enabled me to write a suite of stack-safe recursion schemes that operate on types that can be dissected ssrs.
While the stack safety that these two libraries bring about is awesome, it’s also an ergonomic nightmare. For one, Dissect instances for containers have to be derived, and they’re quite difficult, even impossible (at the moment) when taking into account mutual recursion. A solution that the original paper proposed was polynomial functors: essentially generic types that when put together, allow one to define a data type with a free Dissect instance—though with caveats like having to write “smart” constructors, making it difficult to write pattern matching, and really bad performance.
Though, I’ve invested some time implementing Dissect for Variant, which takes away the complexity of nested Sum types. Likewise, I’ve also managed to approximate mutual recursion using Variant, and here’s a general example with an evaluation catamorphism.
That aside, I’ve been thinking about encoding functional dissections a bit differently for quite a while now. I’ve noticed a pattern that hand-written instances for Dissect have, and it’s that the number of points of recursion that a constructor in a recursive data type has directly corresponds to the number of “states” it has when being dissected. Take for example the following type:
data TreeF n
= Leaf
| Fork n n n
The corresponding structure that I’d have to build for this in order to get a dissection would be:
data TreeF_2 n m
= ForkRR m m
| ForkLR n m
| ForkLL n n
Which gives the following Dissect instance:
instance Dissect TreeF TreeF_2 where
right = case _ of
Left Leaf -> Right Leaf
Left (Fork m n o) -> Left (Tuple m (ForkRR n o))
Right (Tuple w c) -> case w of
ForkRR m n -> Left (Tuple m (ForkLR c n))
ForkLR n m -> Left (Tuple m (ForkLL n c))
ForkLL n o -> Right (Fork n o c)
When a Fork is initially dissected, it yields some m, then ForkRR, which means that there’s 2 items left in the structure. Similarly, if we follow this chain, we see that ForkRR yields another m, and gets transformed into ForkLR, with an item c injected in place of it. ForkLR then goes into ForkLL at which point there’s nothing left to yield, and it instead reconstructs a Fork with all the replacement items carried over from the previous states.
This actually reminds me of Python’s generators, essentially a generalization of iterators that allow for duplex communication. I can send some data to a generator, and get some data back.
In [33]: def example(xs):
...: ys = []
...: for x in xs:
...: y = (yield x)
...: ys.append(y)
...: return ys
...:
In [34]: i = example([1, 2, 3])
In [35]: a, b, c, d = i.send(None), i.send(1), i.send(2), i.send(3)
---------------------------------------------------------------------------
StopIteration Traceback (most recent call last)
<ipython-input-35-9b84b70d7082> in <module>
----> 1 a, b, c, d = i.send(None), i.send(1), i.send(2), i.send(3)
StopIteration: [1, 2, 3]
In this case, a, b, and c now have 1, 2, and 3 respectively, meanwhile at the end of the chain I get an exception carrying the list of all the items that I’ve sent over. Had I structured this a bit more, I’d actually have a way to have a mapping operation.
Translating this onto PureScript was something that I’ve had at the back of my mind for quite a while now, though I’ve been reluctant to explore possible solutions or abstractions that could help translate this over to use with dissections. A monadic interface for this type of duplex communication likely won’t be too complicated, though either doing it through codegen or type classes is a different story.
On that note, it’d be pretty interesting to see a solution that involves generating abstract state machines for each recursive type, like parser generators in a way, though frankly my knowledge on this is particularly limited.
Related Stuff:
Clowns to the Left of me, Jokers to the Right (Pearl)
Original paper where dissect was derived from.
. The generic approach is a total non-starter though IMO, and unfortunately it is excruciatingly tedious to write (especially since it’s totally first order). However it’s really modest in allocations and seems to JIT really well. My suspicion about the generator approach is that you will essentially end up with a Free Monad construction and hit the same performance profile as a trampolined traversal.
