Why does `:kind` in the REPL throw error for `data T a f = T (a f)`?

Help
#1

I was playing around in the REPL trying to understand Data.NonEmpty’s definition, so I came up with the following types and wanted to check their kind(?) when this error popped up:

> import Data.List (List(..), (:))
> 
> data T   f a = T f a    -- ≈ Data.Tuple
> data T'  f a = T' (f a)
> data T'' f a = T'' a (f a)
>
> x = T   1 "a"        :: T   Int String
> y = T'  (1 : Nil)    :: T'  List Int
> z = T'' 27 (1 : Nil) :: T'' List Int
>
> :kind T 
Type -> Type -> Type

> :kind T''
(Type -> Type) -> Type -> Type

> :kind T' 
Error found:
at <internal>:0:0 - 0:0 (line 0, column 0 - line 0, column 0)

  Type variable k is undefined.

while inferring the kind of k
while checking that type k
  has kind Type
while inferring the kind of T' @k

See https://github.com/purescript/documentation/blob/master/errors/UndefinedTypeVariable.md 
for more information, or to contribute content related to this error.

Went to link in the error description, but it does not seem to be related to this one (or I failed to make the connection). As far as I understand, f in data T' f a has to be a functor, so why is :kind unable to infer this, yet it has no problem with T'' (or NonEmpty)?

#2

I can kinda help with this. The issue being bumped into here is called “polymorphic kinds” or “polykinds.” Here’s some references on the matter:

If you add a kind annotation to T':

data T' :: (Type -> Type) -> Type -> Type
data T' f a = T' (f a)

then it’ll work (of course that kinda defeats the purpose of asking the REPL to print the kind information).

I think it otherwise could have kind

data T' :: forall k. (k -> Type) -> k -> Type

I can’t do a good job of explaining why T' needs the annotation and others don’t, and I can’t do a good job of explaining what other k’s you could use to do something useful besides Type.

1 Like
#3

No worries and thank you! You already did plenty as it would have taken me quite a while to stumble upon “polymorphic kinds”… and I didn’t even know about kind signatures…:slight_smile:

#4

T' needs an annotation because the kind of a cannot be unambiguously inferred. It depends on what f is. Which itself depends on what a is.

For example:

> data F a = F a
> :kind T' F
Type -> Type

> data G a = G (a Int)
> :kind T' G
(Type -> Type) -> Type

In these two examples the kinds of a are different. In the first example a :: Type and in the second - a :: Type -> Type. This means that the kind of a has to be polymorphic.

In T this doesn’t happen, because both f and a are used in a position where there would be a datum (e.g. T "foo" 42), and therefore both f and a must be Type. No polymorphism.

In T'' this doesn’t happen, because a is used in a data position, and therefore a :: Type, and then f a is used in a data position, and therefore f a :: Type, and therefore f :: Type -> Type. No polymorphism here either.

What fascinates me is why REPL can’t show the polymorphic kind. This works fine at the type level:

> f x = x + zero
> :t f
forall (a25 :: Type). Semiring a25 => a25 -> a25

And the compiler itself is even able to figure this out when in IDE support mode:

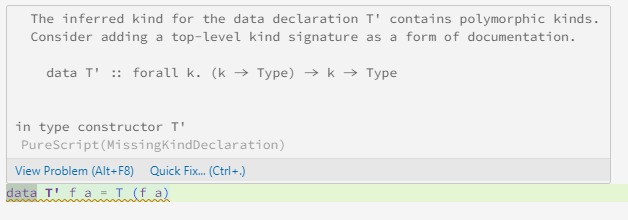
image

(and, of course, when compiling)

So why not in REPL?

3 Likes